- Details
- Hits: 139
Authors: A. R. ALIEV, N. L. MURADOVA

Keywords: operator-differential equation, smooth solution, self-adjoint operator, Hilbert space, intermediate derivative operators
DOI: https://doi.org/10.32010/j.bmj.2022.01
- Details
- Hits: 136
Authors: E. H. KHALILOV
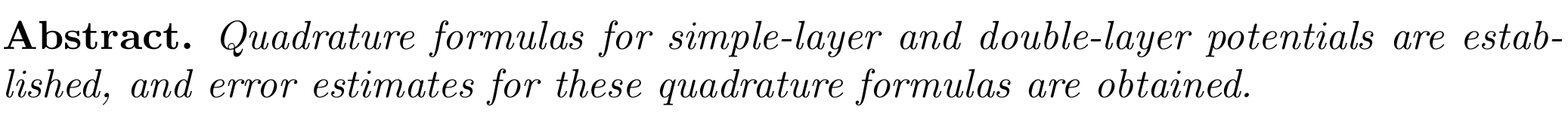
Keywords: quadrature formulas, simple-layer potential, double-layer potential, Hankel function, curvilinear integral, Lyapunov curve
DOI: https://doi.org/10.32010/j.bmj.2022.02
- Details
- Hits: 132
Authors: V. M. ABDULLAYEV, S. S. JAFARLI, Y. M. MEHDIYEV
Abstract. In this work, a class of optimal control problems for a rod (plate) heating process with feedback, when the incoming information about the state of the process is continuously received only from its individual points, at which some temperature sensors are placed, is investigated. The heating process itself takes place in a stove at the expense of controlling the temperature inside the stove. The mathematical model of the controlled process is in both cases described by a punctual loaded parabolic type equation. In the work, we derive formulae for the gradient of the functional. Algorithms of numerical solutions to the considered problems are proposed.
Keywords: optimal control, principle of maximum, loade differential equations, non-separated conditions
DOI: https://doi.org/10.32010/j.bmj.2022.03
- Details
- Hits: 121
Authors: J. J. HASANOV, Z. V. SAFAROV
Abstract. The aim of this paper is to prove the Hardy-Littlewood-Stein-Weiss theorems for Riesz potentials in modified Morrey spaces
Keywords: maximal operator, fractional maximal operator, Riesz potential, weighted modified Morrey space
DOI: https://doi.org/10.32010/j.bmj.2022.04
- Details
- Hits: 118
Authors: L. I. MAMMADOVA, I. M. NABIEV
Abstract. In the article we consider the Sturm-Liouville operator with semiseparated boundary conditions, one of which contains a spectral parameter. An asymptotic formula for the eigenvalues of the operator under consideration is given and a uniqueness theorem for the solution of the inverse problem of recovering the corresponding boundary value problems is proved.
Keywords: Sturm-Liouville operator, eigenvalues, inverse problem, uniqueness theorem
DOI: https://doi.org/10.32010/j.bmj.2022.05
- CORRECT PROOF OF FINDING THE EXACT LOWER BOUND OF THE RAYLEIGH MAGNETIC VALUE
- A MIXED PROBLEM FOR A ONE-DIMENSIONAL VISCOELASTICITY EQUATION WITH NON-STATIONARY CONJUGATION CONDITIONS
- INVERSE PROBLEM FOR RECONSTRUCTING THE RIGHT SIDE OF A ONE-DIMENSIONAL WAVE EQUATION
- SYNTHESIS OF ZONAL CONTROLS USING INFORMATION ON THE OBJECT'S STATE AT THE CURRENT AND PREVIOUS MOMENTS OF TIME
